I wrote this sequence on a napkin a few weeks ago, found I don’t even remember where — it only said “it skips over perfect squares”:
![]()
So what happens? Look at its breakdown:
| 1 | 2 | 2.5 | 2 |
| 2 | 3.1 | 3.6 | 3 |
| 3 | 4.7 | 5.3 | 5 |
| 4 | 6 | 6.5 | 6 |
| 5 | 7.2 | 7.9 | 7 |
| 6 | 8.4 | 8.9 | 8 |
| 7 | 9.6 | 10.1 | 10 |
| 8 | 10.8 | 11.3 | 11 |
This is such a fascinating sequence! How is it possible? How can we prove that it will skip over all perfect squares? This relies on a few facts that I discovered just by investigating this sequence:
- The amount of whole numbers in-between two perfect squares is always even. This is easily proven by
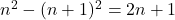 . Because we want it exclusive, i.e. not counting the number we land on, we still need to take away 1, which gives
. Because we want it exclusive, i.e. not counting the number we land on, we still need to take away 1, which gives 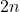 .
. - Of this even amount, the integer part of
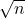 is constant. Moreover, half of the outputs will be
is constant. Moreover, half of the outputs will be 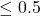 and half
and half 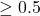 . That’s because half of the inputs are smaller than the inputs midpoint, and half are greater. And because
. That’s because half of the inputs are smaller than the inputs midpoint, and half are greater. And because 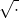 is monotonically increasing, order is preserved.
is monotonically increasing, order is preserved. - The first output to exceed
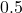 in its decimal part gets bumped to the next integer by the
in its decimal part gets bumped to the next integer by the 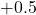 of the formula.
of the formula.
