It doesn’t happen often that I come across an interesting problem on student’s homework. This one was.
You take a loan for 1000$ with an interest rate of 20% per month. What is your debt after six months?
Obviously the textbook contains the exact formula the student should use to just show that He Knows It, but we’re here for the exploration so we’ll act as if we didn’t know anything other than basic arithmetic.
After the first month, the debt 
is
![\[d(1) = \text{base amount} + \text{interests after 1 month} = 1000 + \dfrac{20}{100} 1000 = 1200\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-cff9aad0cdc94a2da98f9f76afadb6ea_l3.png "Rendered by QuickLaTeX.com")
After two months,
(1) 
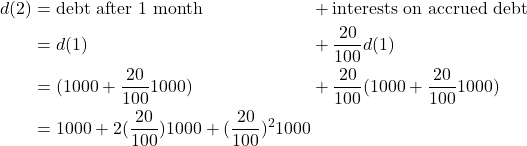
After three months, the reasoning is similar but we have to be careful not to infer the wrong pattern. In fact, it is tempting to say that 
will be the same as 
except that all 
s will be swapped with 
s, but that would be wrong. If we do the calculation once more, we find
![\[d(3) = 1000 + 3 (\dfrac{20}{100}) 1000 + 3 (\dfrac{20}{100})^2 1000 + (\dfrac{20}{100})^3 1000\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-9a433be40c500811b9f0b15d56340869_l3.png "Rendered by QuickLaTeX.com")
if you haven’t collapsed into a coma and feel like doing it one more time,
![\[d(4) = 1000 + 4 (\dfrac{20}{100}) 1000 + 6 (\dfrac{20}{100})^2 1000 + 4 (\dfrac{20}{100})^3 1000 + (\dfrac{20}{100})^4 1000\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-64edfd72245b81aa352f09e11cfede8c_l3.png "Rendered by QuickLaTeX.com")
do the coefficients ring a bell? It’s a Pascal’s triangle. And it makes sense, as the next term is the sum of the previous term plus the previous term times its own base power 
. That mixes the terms in just the right way so that they line up perfectly.
So the pattern is
![\[d(n) = \sum_{k=0}^n \binom{n}{k} (\dfrac{20}{100})^k 1000\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-90d2533f294873d11c121501c39e554b_l3.png "Rendered by QuickLaTeX.com")
That’s one way, and it gets us somewhere. Now let’s try another road and see how stupid it is and how much of a difference it can make. Think of grouping for 1000:
![\[d(1) = 1000 + \dfrac{20}{100} 1000 = 1000(1 + 0.2)\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-db01654c9fb09129f8071d9eaca968be_l3.png "Rendered by QuickLaTeX.com")
![\[d(2) = d(1) + \dfrac{20}{100} d(1) = 1000(1 + 0.2) + 0.2 \cdot 1000(1 + 0.2) = 1000(1 + 2 \cdot 0.2 + 0.2^2) = 1000(1 + 0.2)^2\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-9e42d27225beffaf2728e07e1c2ac307_l3.png "Rendered by QuickLaTeX.com")
![\[d(3) = d(2) + \dfrac{20}{100} d(2) = ... = 1000(1 + 3 \cdot 0.2 + 3 \cdot 0.2^2 + 0.2^3) = 1000(1 + 0.2)^3\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-d5d48f448b7d9952c810d9e2e2f749d9_l3.png "Rendered by QuickLaTeX.com")
The pattern here is much more obvious:
![\[d(k) = 1000(1+0.2)^k\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-3e18a4254a8bd3ee9c7cf4e9ac67ead6_l3.png "Rendered by QuickLaTeX.com")
which is what the poor children are thought: the debt at month 
is the base sum times 
.
It takes nothing to see how quickly it gets out of control. With such a simple formula, it’s possible to ask all sort of questions. For example,
How many months does it take for my debt to double?
![\[\text{For which } k \in \mathbb{N} \text{does} d(k) = 2000? \Rightarrow 2000 = 1000(1.2)^k \Rightarrow k = \log_{1.2}(2) \approx 3.8\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-309e49da5d7c9e64cc729e776bca8fb8_l3.png "Rendered by QuickLaTeX.com")
so in just about 4 months I’m twice as in debt as I was when I was careless and free. Incredible, few teenagers would believe it.
How much do I have to pay every month so that my debt stays fixed and doesn’t grow?
This is trickier. If we think too narrowly, we may end up imposing
![\[d(k) = 1000 \ \forall k \in \mathbb{N} \Rightarrow 1000(1.2)^k = 1000 \ \forall k\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-6d56ca1589e0fa5d6086817465c86f01_l3.png "Rendered by QuickLaTeX.com")
And this only works in the first month, for 
. Instead, in the first month the debt will grow, and there’s nothing we can do about it. We need to allow the debt to grow somewhat before we can control it, otherwise we simply wouldn’t take a loan in the first place: we needed those 1000$ that month, and the bank will charge us a fee for having given that upfront. So we’ll get to 
. The question is how do we stay fixed at 1200$, and not grow beyond it? How can be equal to ?
Well, the question is not quite right. Debt is a thing that evolves constantly, and we can’t bound it month by month. But we can ensure it doesn’t grow beyond a certain point:
![\[(1200 - \text{payback})(1.2) = 1200 \Rightarrow \text{payback} = \dfrac{1200 \cdot 0.2}{1.2} = 200\]](https://quickmathintuitions.org/wp-content/ql-cache/quicklatex.com-6fa6503f204f252db543a58f01228124_l3.png "Rendered by QuickLaTeX.com")
which is not quite mindblowing: if every month we accrue 200$ of debt, if we pay them back we get back to the original first month state. But it’s an unstable balance: as soon as this get past the first month and beyond 1200$, then we’d need to recalculate.
