In words, an equation is a technique to figure out the value of a quantity when the only thing we have is a convoluted and self-referential definition. Enough talking, now to the action.
Imagine somebody comes with this riddle-sounding problem:
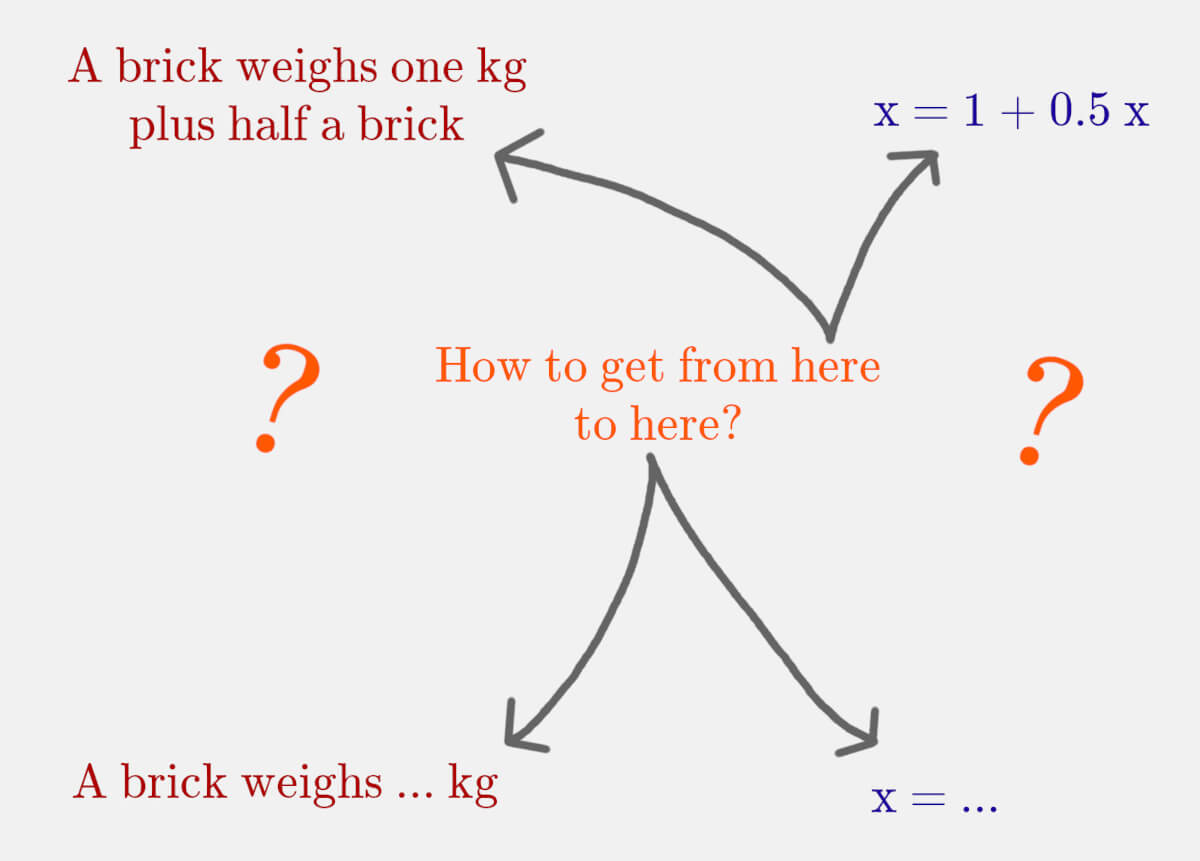
A brick weighs as much as a kilo plus half a brick. How much does a brick weigh?
How can we tell how much a brick weigh if its weight is defined in terms of bricks? This seems hopelessly circular.
Let’s look at the problem statement and try to clean it up, to reduce it to its bare bones.
So that in the end the problem statement reads like:
It definitely reads mathy, although not properly equationy yet. Not intimidating enough. But from here on, the path is the same: keep simplify and shortening, and load each symbol with more and more meaning.
We know we’re talking bricks here, and we only need be passingly reminded, so we can make one further shortening:
We also know we’re talking weight, and we’ll leave the 
sign to carry its full meaning of “weighs as much as”, so that we can drop the kg reference:
We can also agree that every time there’s 
beside the letter 
, we’ll omit it:
And an equation is born. Oh wait, we’ve missed a step. What’s an equation without an 
? Just swap all the for (only because it’s a convention to use the last few letters of the alphabet for unknowns quantities):
Now this, this is an equation your math teacher could be proud of, where is the unknown. In truth, we’ve been doing equations since the very first statement: what authority is telling us we can’t use 
in an equation, in place of the ? Who said we can’t have 
in it? Or words like 
? Why do we want to make our life so complicated?
Well, look what happens if we take the following equation and put in all the words:
A brick plus seven fifths of a kg plus half a brick weighs as much as half a brick plus five kilos.
Sooo long, and clunky. Plus, it’s ambiguous: “half a brick plus five kilos” could be both a) first adding together a brick and 5 kilos and then taking half of the whole thing, or b) taking half a brick first and then adding 5 kilos to that. And this is one of the simplest equations you could come up with: the amount of ambiguity grows and grows the more information you add. We cannot afford any ambiguity: even the slightest difference changes the final result. Language is poetic and flexible, but is not rigorous and unambiguous: for that, there’s math with its symbols and equations. Math is the language humanity has come up to unambiguously convey information, to take one very precise idea from one mind and transfer it to another mind without altering its shape one bit. In the recent history of natural language we’ve also tried to address the problem by adding punctuation, but that still falls short with the high precision standard that technical subjects require. The size of a nail can cause an Apollo mission to fail.
Going back and forth a problem’s statement in natural language and in math symbols is extremely valuable when learning math, as it teaches math as a language, rather than a set of abstract symbols. During my first year of high school my teacher would have us all describe math statement in natural language, or to dictate to him an equation from the textbook, spelling it out in natural language. It was tedious, and valuable, and an exercise I recommend in education.
How to solve an equation
Alright, now we know what an equation is and how one is born. Let’s get back to what we’ve built so far:
It seems hopelessly circular still, with on both sides of the equal. It is true: so far we haven’t done anything other than shortening and dropping words, so the problem is unaltered! Not much creativity or smartness has happened so far. Now we’ll draw from the standard math mindset that will lead us oh so far in life:
- think about where we want to get, what our goal is;
- figure out how we can get there.
Print those two points out on a giant poster and stick it into your child’s bedroom. Every theorem in math first describes the starting point, then sets out the ending goal, and finally explains how you can get there. The where requires clarity of mind, the how takes creativity and ideas. Math exploration is not as tidy, because you don’t always know if you can get where you’d like to get, so you often wander a bit around exploring where you can get from where you stand, and figuring out your goals as you walk around, charting the map of your territory.
But I digress. Always think where you want to get, and how you can get there. To get where you want, you often need to leap into a different realm.
Our goal is obtaining a statement that would read like “A brick weighs … kg”, or, in math terms, 
. When we get to this formulation, we can easily read out the weight of a brick. How do we get there?
Ideas in math are often hidden in plain sight — or rather, they are part of the scenery, so you have to spot them in the smallest of details. We’re talking weight. How about scales?
Our statement suggests that if we load a scale with one brick on one side and half a brick and a kilo on the other, it will be in balance.
What do we know about scales? I’m gonna pretend word meaning is meaningful, and say they scale: 100 grams weigh as much as 100 grams, 80 grams weigh as much as 80 grams. It’s an obvious and useless remark, but a rephrasing suddenly makes it much more useful: if we alter the amount of weight on both sides at the same time, the scale is still in balance. If we add, subtract, divide, or multiply the same quantity to both sides, the scale stays in balance.
Now think again where we want to get and how that translates into scales: we want one side of the scale to only contain bricks, and the other to only contain kilos. From here onward, the math dopamine kick wears off and it’s all downhill. If we take away half a kilo from both sides, we get where we want (almost).
There’s only a minor annoyance here: we’ve now discovered that half a brick weighs as much as a kilo, but we were actually interested in full bricks. Well, we can scale the quantities, doubling them both. And hopefully it doesn’t then take a leap of faith in accepting that two half bricks make a whole brick.
