On the relationship between L^p spaces and C_c functions for p = infinity

Very quick post on the relationship between $\mathcal{L}^p$ , $\mathcal{C}_c(X)$ and $\mathcal{L}^\infty$ . I will assume you already know what I am talking about, I’ll just be sharing some intuition on what those mean, but won’t bother with details. It’s more a reminder for me rather than something that intends to be useful, actually, but there’s almost nothing on the Internet about this!

When we discover that $\mathcal{C}_c(X)$ (continuous functions with compact support) is dense in $\mathcal{L}^p$ , we also discover that it does not hold if $p = \infty$ and $\mu(X) = \infty$ .

What that intuitively means is that if you take away functions in $\mathcal{C}_c(X)$ from $\mathcal{L}^p$ , you take away something fundamental for $\mathcal{L}^p$ : you are somehow taking away a net that keeps the ceiling up.

The fact that it becomes false for limitless spaces ( $\mu(X) = \infty$ ) and $p = \infty$ means that the functions in $\mathcal{L}^\infty$ do not need functions in $\mathcal{C}_c(X)$ to survive.

This is reasonable: functions in $\mathcal{L}^\infty$ are not required to exist only in a specific (compact) region of space, whereas functions in $\mathcal{C}_c(X)$ do. Functions in $\mathcal{L}^\infty$ are simply bounded – their image keeps below some value, but can go however far they want in x direction. Very roughly speaking, they have a limit on their height, but not on their width.

What we find out, however, is that the following chain of inclusions holds:

$\mathcal{C}_c(X) \subset \mathcal{C}_\infty(X) \subset \mathcal{L}^\infty$

That’s reasonable! Think about it:

Functions in 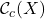$\mathcal{C}_c(X)$ live in a well defined area of space – a confined area of space.
Functions in 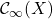$\mathcal{C}_\infty(X)$ are allowed to live everywhere, with the constraint that they become more and more negligible the farther and farther we go. Not required to ever be zero though.
Functions in 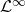$\mathcal{L}^\infty$ are simply required to have an upper bound (a finite one, obviously).

I’m not saying this is simple (advanced analysis is at least as difficult as pitching a nail with a needle as hammer), but after careful thinking, it’s just the way it should be, given the definitions.

Was this Helpful ?
yes no

On the relationship between L^p spaces and C_c functions for p = infinity

Leave a Reply Cancel reply

Categories

Blog entries