In linear algebra it is sometimes needed to find the equation of the line of shortest distance for two skew lines. What follows is a very quick method of finding that line.
Let’s consider an example. Start with two simple skew lines:
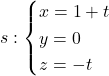
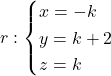
(Observation: don’t make the mistake of using the same parameter for both lines. Each lines exist on its own, there’s no link between them, so there’s no reason why they should should be described by the same parameter. If this doesn’t seem convincing, get two lines you know to be intersecting, use the same parameter for both and try to find the intersection point.)
The directional vectors are:
![]()
So they clearly aren’t parallel. They aren’t incidental as well, because the only possible intersection point is for ![]() , but when
, but when ![]() ,
, ![]() is at
is at ![]() , which doesn’t belong to
, which doesn’t belong to ![]() . It does indeed make sense to look for the line of shortest distance between the two, confident that we will find a non-zero result.
. It does indeed make sense to look for the line of shortest distance between the two, confident that we will find a non-zero result.
The idea is to consider the vector linking the two lines in their generic points and then force the perpendicularity with both lines.
We will call the line of shortest distance ![]() . In our case, the vector between the generic points is (obtained as difference from the generic points of the two lines in their parametric form):
. In our case, the vector between the generic points is (obtained as difference from the generic points of the two lines in their parametric form):
![]()
Imposing perpendicularity gives us:
![]()
![]()
Solving the two simultaneous linear equations we obtain as solution ![]() .
.
This solution allows us to quickly get three results:
- The equation of the line of shortest distance between the two skew lines: just replace
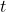 and
and 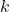 in
in 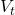 with the values found. In our case,
with the values found. In our case, 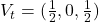 .
. - The intersection point between
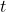 and
and  : just replace
: just replace 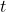 in the parametric equation of
in the parametric equation of  . In our case,
. In our case, 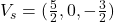 .
. - The intersection point between
 and
and  : just replace
: just replace  in the parametric equation of
in the parametric equation of  . In our case,
. In our case, 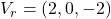 .
.
Do you have a quicker method? Share it in the comments!
