Statistical hypothesis testing is really an interesting topic. I’ll just briefly sum up what statistical hypothesis testing is about, and what you do to test an hypothesis, but will assume you are already familiar with it, so that I can quickly cover a couple of A-HAs moments I had.
In statistical hypothesis testing, we
- have some data, whatever it is, which we imagine as being values of some random variable;
- make an hypothesis about the data, such as that the expected value of the random variable is
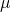; - find a distribution for any affine transformation of the random variable we are making inference about – this is the test statistic;
- run the test, i.e. numerically say how much probable how observations were in relation to the hypothesis we made.
I had a couple of A-HA moments I’d like to share.
There is a reason why this is called hypothesis testing and not hypothesis choice. There are indeed two hypothesis, the null and the alternative hypothesis. However, their roles are widely different! 90% of what we do, both from a conceptual and a numerical point of view, has to do with the null hypothesis. They really are not symmetric. The question we are asking is “With the data I have, am I certain enough my null hypothesis no longer stands?” not at all “With the data I have, which of the two hypothesis is better?”
In fact, the alternative hypothesis is only relevant in determining what kind of alternative we have: whether it’s one-sided (and which side) or two-sided. This affects calculations. But other than that, the math doesn’t really care about the specific value of the alternative. In other words, the two following test are really equivalent:
This accounts for why, when evaluating a p-value, we refuse the null hypothesis only for very low figures. The way I first thought about it had been: “Well, the p-value is, intuitively, a measure of the proximity of the observed data to the null hypothesis. Then, if I get something around 
, I should refuse the null hypothesis and switch to the alternative, as it seems a better theory.” But this is a flawed argument indeed. To see if the alternative was really better I should run a test using it as principal hypothesis! We refuse for very low p-values because that means we null hypothesis really isn’t any more good, and should be thrown to the bin. Then we need to care about finding another good theory that can suit the data.
However, before throwing the current theory out of the window, we don’t accept all kinds of evidence against it: we want a very strong evidence. We don’t want to discard the current theory for another that could only be marginally better. It must be crushingly better!
