This is taken from my Master Thesis on Homomorphic Signatures over Lattices.
See also But WHY is the Lattices Bounded Distance Decoding Problem difficult?.
What are homomorphic signatures
Imagine that Alice owns a large data set, over which she would like to perform some computation. In a homomorphic signature scheme, Alice signs the data set with her secret key and uploads the signed data to an untrusted server. The server then performs the computation modeled by the function 
to obtain the result 
over the signed data.
Alongside the result 
, the server also computes a signature 
certifying that is the correct result for 
. The signature should be short – at any rate, it must be independent of the size of 
. Using Alice’s public verification key, anybody can verify the tuple 
without having to retrieve all the data set nor to run the computation on their own again.
The signature is a homomorphic signature, where homomorphic has the same meaning as the mathematical definition: ‘mapping of a mathematical structure into another one in such a way that the result obtained by applying the operations to elements of the first structure is mapped onto the result obtained by applying the corresponding operations to their respective images in the second one‘. In our case, the operations are represented by the function 
, and the mapping is from the matrices 
to the matrices 
.
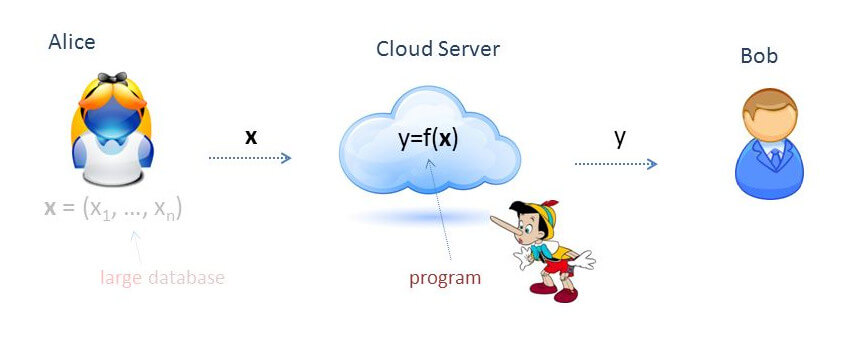
Notice how the very idea of homomorphic signatures challenges the basic security requirements of traditional digital signatures. In fact, for a traditional signatures scheme we require that it should be computationally infeasible to generate a valid signature for a party without knowing that party’s private key. Here, we need to be able to generate a valid signature on some data (i.e. results of computation, like ) without knowing the secret key. What we require, though, is that it must be computationally infeasible to forge a valid signature 
for a result 
. In other words, the security requirement is that it must not be possible to cheat on the signature of the result: if the provided result is validly signed, then it must be the correct result.
The next ideas stem from the analysis of the signature scheme devised by Gorbunov, Vaikuntanathan and Wichs. It relies on the Short Integer Solution hard problem on lattices. The scheme presents several limitations and possible improvements, but it is also the first homomorphic signature scheme able to evaluate arbitrary arithmetic circuits over signed data.
Def. – A signature scheme is said to be leveled homomorphic if it can only evaluate circuits of fixed depth 
over the signed data, with being function of the security parameter. In particular, each signature 
comes with a noise level 
: if, combining the signatures into the result signature 
, the noise level grows to exceed a given threshold 
, then the signature is no longer guaranteed to be correct.
Def. – A signature scheme is said to be fully homomorphic if it supports the evaluation of any arithmetic circuit (albeit possibly being of fixed size, i.e. leveled). In other words, there is no limitation on the “richness” of the function to be evaluated, although there may be on its complexity.
Let us remark that, to date, no (non-leveled) fully homomorphic signature scheme has been devised yet. The state of the art still lies in leveled schemes. On the other hand, a great breakthrough was the invention of a fully homomorphic encryption scheme by Craig Gentry.
On the hopes for homomorphic signatures
The main limitation of the current construction (GVW15) is that verifying the correctness of the computation takes Alice roughly as much time as the computation of itself. However, what she gains is that she does not have to store the data set long term, but can do only with the signatures.
To us, this limitation makes intuitive sense, and it is worth comparing it with real life. In fact, if one wants to judge the work of someone else, they cannot just look at it without any preparatory work. Instead, they have to have spent (at least) a comparable amount of time studying/learning the content to be able to evaluate the work.
For example, a good musician is required to evaluate the performance of Beethoven’s Ninth Symphony by some orchestra. Notice how anybody with some musical knowledge could evaluate whether what is being played makes sense (for instance, whether it actually is the Ninth Symphony and not something else). On the other hand, evaluating the perfection of performance is something entirely different and requires years of study in the music field and in-depth knowledge of the particular symphony itself.
That is why it looks like hoping to devise a homomorphic scheme in which the verification time is significantly shorter than the computation time would be against what is rightful to hope. It may be easy to judge whether the result makes sense (for example, it is not a letter if we expected an integer), but is difficult if we want to evaluate perfect correctness.
However, there is one more caveat. If Alice has to verify the result of the same function over two different data sets, then the verification cost is basically the same (amortized verification). Again, this makes sense: when one is skilled enough to evaluate the performance of the Ninth Symphony by the Berlin Philharmonic, they are also skilled enough to evaluate the performance of the same piece by the Vienna Philharmonic, without having to undergo any significant further work other than going and listening to the performance.
So, although it does not seem feasible to devise a scheme that guarantees the correctness of the result and in which the verification complexity is significantly less than the computation complexity, not all hope for improvements is lost. In fact, it may be possible to obtain a scheme in which verification is faster, but the correctness is only probabilistically guaranteed.
Back to our music analogy, we can imagine the evaluator listening to a handful of minutes of the Symphony and evaluate the whole performance from the little he has heard. However, the orchestra has no idea at what time the evaluator will show up, and for how long they will listen. Clearly, if the orchestra makes a mistake in those few minutes, the performance is not perfect; on the other hand, if what they hear is flawless, then there is some probability that the whole play is perfect.
Similarly, the scheme may be tweaked to only partially check the signature result, thus assigning a probabilistic measure of correctness. As a rough example, we may think of not computing the homomorphic transformations over the 
matrices wholly, but only calculating a few, randomly-placed entries. Then, if those entries are all correct, it is very unlikely (and it quickly gets more so as the number of checked entries increases, of course) that the result is wrong. After all, to cheat, the third party would need to guess several numbers in 
, each having 
likelihood of coming up!
Another idea would be for the music evaluator to delegate another person to check for the quality of the performance, by giving them some precise and detailed features to look for when hearing the play. In the homomorphic scheme, this may translate in looking for some specific features in the result, some characteristics we know a priori that must be in the result. For example, we may know that the result must be a prime number, or must satisfy some constraint, or a relation with something much easier to check. In other words, we may be able to reduce the correctness check to a few fundamental traits that are very easy to check, but also provide some guarantee of correctness. This method seems much harder to model, though.
