Systems of equations are an evolution of equations, but they are often misunderstood. This article aims at providing real world examples and intuitions for systems of equations, and in particular for overdetermined and undetermined systems.
Intuition for systems of equations
Intuitively, we can think of a system of equations as a set of requests. Let’s imagine to have a group of people in front of us, and to have to give a task to each of them. An informal example system could be the following:
- Anna, solve a system of linear equations;
- George, go to the beach and have fun;
- Luke, prevent Anna from ringing social services.
In this form, a solution to the system consists in a list of pairings person-task that satisfies the demands detailed above. In other words, giving a solution to the system amounts to saying what Anna should do, what George should do, and what Luke should do, so that the demands are satisfied. In the example above, Anna should solve a system of equations, George should go to the beach, and Luke should prevent Anna from ringing social services.
It seems pretty obvious, but this intuition will be useful when covering over/underdetermined systems.
Overdetermined systems of equations
Let’s think of having to give orders to a large number of people. It might happen that, when getting to the last person, we forget to whom we have already given an order and to whom not, and we might end up repeating some orders:
- Anna, do the laundry;
- George, go to the beach;
- Luke, get Anna’s laundry dirty;
- Sophie, prevent Luke from dirtying the laundry;
- …
- George, go to the beach.
Here George has received his order twice. In these cases, we say that the system is overdetermined, because it has more orders than people. The example above is innocuous, because George is simply told to the same thing twice. The simplest mathematical example of such a system is when two equations are proportional to each other:
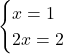
This is an overdetermined system with a solution: 
. The second equation is just redundant, like a game in which the second rule states to follow the first.
How about the following instead:
- Anna, do the laundry;
- George, go to the beach;
- Luke, get Anna’s laundry dirty;
- Sophie, prevent Luke from dirtying the laundry;
- …
- George, bake a cake.
Here George gets two clashing orders, and is rightfully confused: he cannot go to the beach and bake a cake at the same time. He is going to disappoint us no matter what. Indeed, this system is not only overdetermined, because there are more orders than people, but is also without solution. In fact, we are unable to come up with a list of pairings people-tasks as before. If George would go to the beach, he would be ignoring the baking order; if he would bake a cake, he would be ignoring the beach order. There is no way out: there is no solution! It is a bit like a game where the second rule says not to follow the first: it is impossible to play a game like that!
The simplest mathematical example of such a system is:
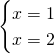
which does not have a solution because we ask 
to be 
and 
at the same time — a bit like asking your neighbor to be male and female at the same time (but not queer).
So once again: when a system of equations has more equations than unknowns, we say it is overdetermined. It means that too many rules are being imposed at once, and some of them may be conflicting. However, it is false to state that an overdetermined system does not have any solution: it may or it may not. If the surplus commands are just reformulations of other orders, then it is not a problem: the system does have a solution.
Underdetermined systems of equations
If we give less orders than the number of people, we say the system is underdetermined. When this happens, at least one person must have not received any command. This time, the idea is that people who do not receive any command are free to do whatever they want.
For example, let’s imagine again to have Anna, George, and Luke lined in front of us. If our commands are:
- Anna, do the laundry;
- George, go to the beach.
then Luke has not received any order. Maybe he will go to the park, maybe he will prevent Anna from ringing social services… he is free to do whatever he wants: the options are infinite! In these cases, we say that Luke is a free variable. As long as Anna and George stick to what they are told, each of Luke’s options makes for a solution: that is why the system has an infinite number of solutions.
As a mathematical example, think of being asked to find values for 
satisfying the following system:
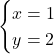
great, but what about 
? Here is a free variable and solutions are infinite.
However, there can also be undetermined systems with no solution. That is the case when we give too few orders, and some of them are conflicting with each other. Again with our favorite trio:
- Anna, do the laundry;
- George, go to the beach;
- Anna, go to the park.
Not only are we not saying anything to Luke here, but we are also giving clashing orders to Anna. So even if the absence of commands to Luke would allow infinite solutions, Anna’s impossibility to satisfy the constraints makes it so that no solution exists.
Examples and final remarks
All in all, there are no strict rules. What appears to be an overdetermined system could turn out to be an underdetermined one, and an underdetermined system could have no solution.
Finally, notice that in mathematical reality commands usually address more than one person at a time. A system of equations in real life is something like:
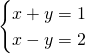
Here the intuition gets trickier, because each command mixes at least two people, and is hard to render in natural language. Still, the orders analogy is useful in understanding what underdetermined and overdetermined systems are and why they have infinite or no solutions.
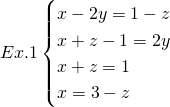in 
An apparently overdetermined system which is actually underdetermined and does not even have a solution.
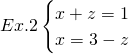in
An overdetermined which does not have a solution.
